1.2) Representation of Decimal number system by binary language
From the previous lesson, we have known how to speak to a computer. Now, we need to know how to convert our language to a binary language (i.e., to zeros and ones). So, let’s start by learning how to convert numbers to zeros and ones. However, we need to know how number systems works, by knowing how decimal number system works.
1.2.1) Number systems:
When we say that we will start learning how to convert numbers to zeros and ones, you will think that we will convert decimal numbers to zeros and ones.
Yes. You are right. However, you must consider two points:
- The binary language has only two numbers; hence, it is called a binary number system.
- We will not limit ourselves to the conversion from the decimal number system to the binary number system, but you will see that many other number systems are used in computer science.
There are a lot of number systems. You can see a list of them through this link (click here).
However, we only care about the number systems found in the next table:
| Number systems | Base/Radix | Symbols |
|---|---|---|
| Decimal | 10 | 0,1,2,3,4,5,6,7,8,9 |
| Binary | 2 | 0,1 |
| Ternary | 3 | 0,1,2 |
| Octal | 8 | 0,1,2,3,4,5,6,7 |
| Hexadecimal | 16 | 0,1,2,3,4,5,6,7,8,9, A, B, C, D, E, F |
In this table, you can see 5 number systems.
The word “base” means how many digits the number system contains. So, the decimal number system is called decimal because its base is 10, which means it consists of 10 digits: 0 to 9.
The same is true in the case of the binary system. Its base is 2 because it has 2 numbers: 0 and 1.
Also, the base of the ternary number system is 3 because it has 3 numbers: 0 to 2.
The base of the octal number system is 8 because it has 8 numbers: 0 to 7.
However, in the case of the hexadecimal number system, the base is 16, which means it has 16 digits: 0 to 15. The problem is that the digits from 10 to 15 are not a one-digit number. For example, 15 is a number that consists of two digits.
The difference between a digit and a number is that a digit consists of only one symbol; 0 to 9, while a number consists of more than one symbol (let’s say, a digit). So, we cannot consider 15 as a one-digit number inside the hexadecimal number system. To solve this problem, we substitute letters for numbers from 10 to 15, as follows:
A = 10, B = 11, C = 12, D = 13, E = 14, F = 15
So, are we able to convert from any number system to binary or decimal number systems? Of course, you can convert from any number system to another. This is what you will see in this chapter.
However, to be able to convert from one number system to another, you need to know the general rules by which any number system works.
We can conclude this general rule from the decimal number system. We will call this general rule the base-n number system rule.
1.2.1.1) Decimal number system:
First, we agree that the decimal number system has 10 digits: 0 to 9, hence the name decimal. Also, we can call it the base-10 number system.
a) How does the decimal number system work?
Let’s take an integer as an example. Say 159. This number consists of 3 digits; 1, 5, and 9 (We have known the difference between number and digit).
Each digit has a weight according to its position. Let’s see the next table:
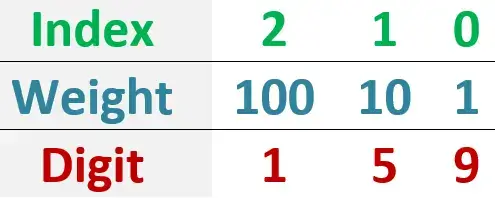
The index represents the position of each digit. Note that we start by numbering the positions from right to left.
As you can see, digit 9 is in the position (i.e., index 0) associated with the value 1, digit 5 is in the position (i.e., index 1) associated with the value 10, and digit 1 is in the position (i.e., index 2) associated with the value 100.
To illustrate that, we can write the following:
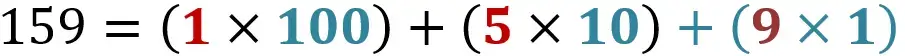
As you can see, each weight equals the weight of its right weight multiplied by 10.
The value of the entire expression is obtained by multiplying each digit by the weight associated with the digit’s position and then adding those products.
We can rewrite this more technically as follows:

You can see that the value has not changed. So, we can rewrite the previous table as follows:
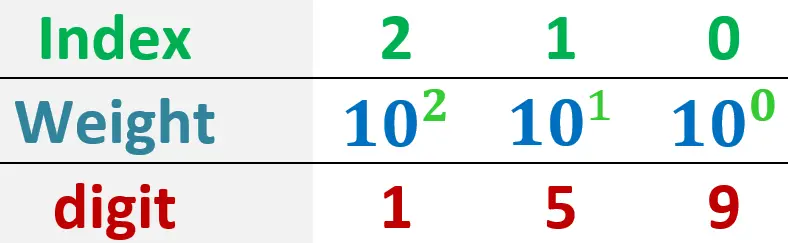
As you can see, the weight of each digit equals the base of the number system raised to the power of the index of the digit.
So, what about the fractional part? So, let’s add a fraction to the previous example. Say 159.25.
In the fractional part, we will change the index. We start numbering the index from -1 (not zero) and continue numbering from left to right.
Why is the index negative in the fractional part? Because the fractional part results from the division by 10 or a multiple of ten.
So, in the fractional part, each weight equals the weight of its left weight divided by 10.
This means that we can rewrite the technical notation as follows:
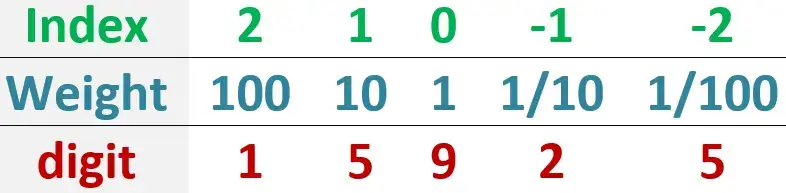
We can rewrite the technical notation as follows:

Did you get it? What can we conclude from this?
- Each digit is multiplied by 10 raised to the power of the digit’s index.
- The index of the integer part starts at 0 and continues from right to left. The index of the fractional part starts at -1 and continues from left to right.
- In the integer part, each weight equals the weight of its right weight multiplied by 10. In the fractional part, each weight equals the weight of its left weight divided by 10.
Why 10?
Because it is the base of the decimal number system, which means that it has 10 numbers: 0 to 9.
b) Extracting the algorithm by which the decimal number system works
Let’s extract a general algorithm by which any number system works.
- We multiply each digit by its weight . This weight equals the base of the number system raised to the power of the index of the digit (let’s denote (i) to index).

- Then, we obtain the value (x) of the entire expression by adding the products of step one.
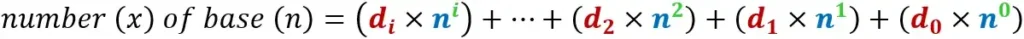
So, we can write
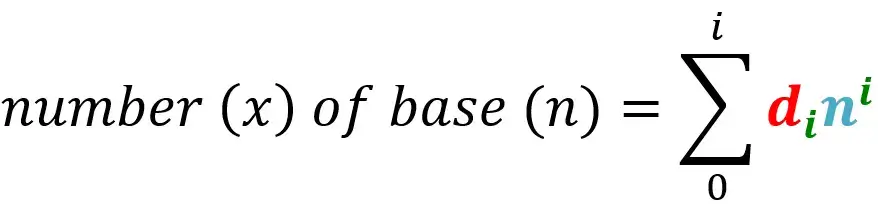
1.2.1.2) Binary number system:
a) Applying the general algorithm of the decimal number system to convert from decimal number system to binary number system:
Let’s apply the general algorithm to the binary number system.
When you apply the general algorithm to any number system, you need to know the base of the number system you apply the algorithm to.
Here, we apply the general algorithm to the binary number system. The base of the binary number system is 2 because it has only 2 digits; 0, and 1 which means that ( n = 2 ).
Suppose that we have a binary number that has only 3 digits, so, we can write the following:

so, let’s simplify the table as follows:
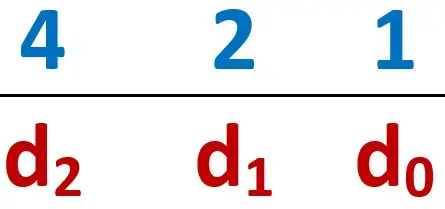
You can replace (d) with the digits of the binary number system. The binary number system has only 2 digits. So, d = {0,1} .
Let’s take examples
Example 1:
What is the equivalent decimal number of the following binary number (100)2?
Solution
| 22 | 21 | 20 |
| 4 | 2 | 1 |
| 1 | 0 | 0 |
(100)_2=(1×2^2 )+(0×2^1 )+(0×2^0 )=4+0+0=(4)_{10}Notice that we wrote 2 as a subscript to the number to illustrate that 100 is a binary number, not a decimal number. The same is true for (4)10. The 10 illustrates that 4 is a decimal number.
Example 2:
What is the equivalent decimal number of the following binary number (110)2?
Solution
| 22 | 21 | 20 |
| 4 | 2 | 1 |
| 1 | 1 | 0 |
(110)_2=(1×2^2 )+(1×2^1 )+(0×2^0 )=4+2+0=(6)_{10}A general and simple rule to convert from the decimal number system to the binary number system is as follows:
From the previous example, we can extract a general and simple algorithm to convert from the decimal number system to the binary number system as follows:
- Write the weight of each digit above it as a base (2) raised to the index of the digit, or by writing 1, starting from the rightmost digit and multiplying each weight by 2 as you go from right to left.
… 8 4 2 1
- Get the summation of the weights associated with the positions occupied by the ones.
Let’s take an example:
Example 3:
What is the equivalent decimal number of the following binary number (1110)2?
Solution
| 23 | 22 | 21 | 20 |
| 8 | 4 | 2 | 1 |
| 1 | 1 | 1 | 0 |
The first step is to write the quantities above the numbers, as shown above. Notice that we start by writing 1 above the rightmost digit then multiply by 2 as we go from right to left.
The second step is to add the quantities occupied by the ones, as follows:
(1110)_2=8+4+2 =(14)_{10}Let’s simplify by using the following table
| × | 8 | 4 | 2 | 1 | |
| 1 | 1 | 1 | 0 | Sum (14)10 | |
| = | 8 | 4 | 2 | 0 |
From the previous example, we say that (100)2 is the bit pattern of (4)10 in the decimal number system, (110)2 is the bit pattern of (6)10, and (1110)2 is the bit pattern of (14)10.
So, what if there is a fractional part in the binary number? Let’s see an example.
Example 4:
What is the equivalent decimal number of the following binary number (1110.01)2?
Solution
| 23 | 22 | 21 | 20 | 2-1 | 2-2 | |
| 8 | 4 | 2 | 1 | ¼ | ||
| 1 | 1 | 1 | 0 | . | 0 | 1 |
You will apply the same method. But in the fractional part, the weights start from ½ from the leftmost digit of the fractional part, then multiply by ½ as you go from left to right.
(1110.01)_2=8+4+2+(1/4) =(14.25)_{10}You can simplify it by using the following table:
| × | 8 | 4 | 2 | 1 | ½ | ¼ | ||
| 1 | 1 | 1 | 0 | . | 0 | 1 | Sum (14.25)10 | |
| = | 8 | 4 | 2 | 0 | 0 | ¼ |
But notice that the decimal point is not stored in memory as a dot. We use it here to learn how to convert from decimal to binary on paper, but there are methods to store the fractional part in memory. We will cover these methods in the course.
