a) Conversion from the decimal number system to the binary number system:

There are three methods:

Successive divisions method:

This is the formal method found in any reference and the one that you use to solve problems in your exams.

Let’s take an example from which we will extract the general algorithm.

Example 9:

What is the equivalent binary number of the decimal number (21.25)₁₀?

We will convert the integer part and fractional part independently.

Conversion of the integer part:

During the conversion from binary to decimal, we were multiplying each binary digit by 2 raised to the power of the index of the digit. So, during the conversion from decimal to binary, we will reverse the process. We will divide the decimal number by 2.

So, how can we do that?

Steps to convert the integer part of the decimal number to binary:

• Step 1: Divide the integer part by 2
• Step 2: Write the remainder in the remainder column and the integer part in the integer column.  If there is no remainder after the division process, then write 0 in the remainder column.
• Step3: Repeat the previous 2 steps until we reach 0.

Let’s apply these steps to this example:

• We divided 21 by 2. Why two? Because it is the base of the binary number system, to which we convert the decimal number. The result of dividing 21 by 2 is 10.5. The result of the division process contains a fraction, so there is a remainder which equals 1. Then, write 1 in the remainder column and 10 in the integer column.
• Then, divide 10 by 2. The result will be 5. There is no fraction this time. Then, write 0 in the remainder column and 5 in the integer column.
• Then, divide 5 by 2. The result is 2.5. This time the result contains a fractional part. Then, write 1 in the remainder column and 2 in the integer column.
• So, divide 2 by 2. The result is 1 without a fraction. So, the remainder is 0 and the integer is 1.
• Finally, divide 1 by 2. This time the integer part is 0, and this marks the end of the division process. The fraction is 0.5, which gives us 1 as a remainder. Generally, the remainder of any fraction is the numerator.

This means that we continue the division process of the integer part by the base of the number system we convert to until the integer part becomes 0.

How to find the remainder easily:

1. Multiply the fractional part that resulted from the division process by 2 (i.e., by the base of the number system). For example, in the first division process, the result is 10.5, so the remainder equals \(0.5\times2=1\).
2. If the numerator is less than the denominator, then the remainder equals the numerator, and the integer part equals 0.

Notice that because you convert to the binary number system, the remainder always equals 0 or 1.

Conversion of the fractional part:

During the conversion from the binary number system to the decimal number system, the fractional part was divided by 2 (i.e., the base of the binary system). So, during the conversion from the decimal number system to the binary number system, we do the reverse process. We multiply the fractional part by 2.

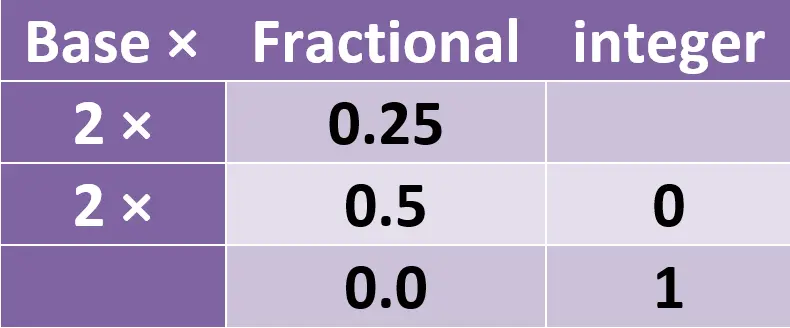
Steps to convert the fractional part of the decimal number to binary:

• Step 1: Multiply the fractional part by 2.
• Step 2: Write the integer part in the integer column and the fractional part in the fraction column.
• Step3: Repeat steps 1 and 2 until we reach 0 or the precision we desire.

Let’s apply these steps to this example:

• The fraction is 0.25. So, \(0.25\times2=0.5\).
• Now, write the integer part to the integer column in the table. Then, continue the multiplication process of the fractional part.
• So, \(0.5\times2=1\). This time the fractional part is 0, which marks the end of the multiplication process.
• Write the integer part in the integer column.

Notice that the integer part is always 0 or 1.

How to write the final result from these tables:

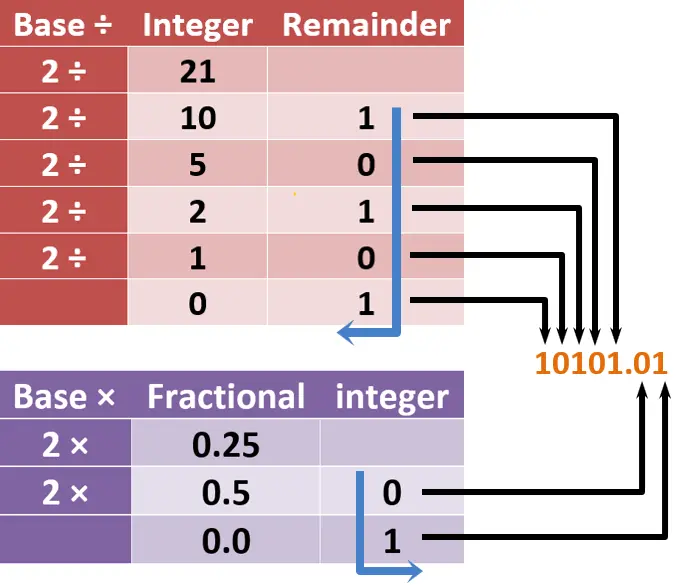
Write the binary number as follows:

First, put the decimal point

______.___

Then, in the integer part table, the remainder column represents the equivalent binary number of the integer part. To write it, start from the top remainder to the bottom one, as shown by the blue arrow. Write the first remainder next to the decimal point, then go from right to left.

In the fractional part table, the integer column represents the equivalent binary number for the fractional part. To write it, start from top to bottom, and write the first integer number next to the decimal point and go from left to right.

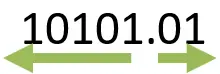
Now, we can write

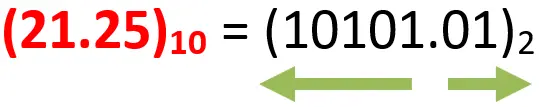
So, what about the conversion of the decimal number to any base number system? The steps are the same except that we will divide by the base of the number system we want to convert to. So, in the following examples, we will not explain all the steps in detail as in the previous example.

b) Conversion from the decimal number system to the ternary number system:

Notice that we use the previous method for the conversion from the decimal number system to any number, except that we change the base according to the number system we convert to.

For example, instead of dividing or multiplying by 2, we will change it to the base of the system we need to convert to.

The Successive division method:

Example 10:

What is the equivalent ternary number of the decimal number (59.39)₁₀?

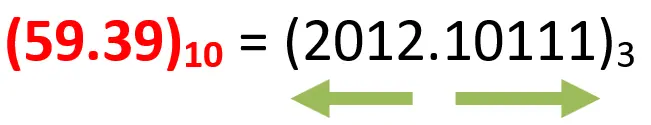
Steps to convert the integer part of the decimal number to ternary:

1. We will divide the integer part by 3 and write the remainder in the remainder column.
2. Continue the division process until you reach \(\frac{2}{3}\). The integer part is 0, which marks the end of the division process, and the fractional part is 2/3 (0.666666). So, the remainder is 2.

How to find the remainder easily:

You can get the remainder by multiplying the fractional part resulting from the division by 3. For example, in the first division, \(\frac{59}{3}=19.666667\). If you multiply the fractional part by 3, then the remainder will be 2.

If you need to know how to get the fractional part in this way, you can watch the video on our channel to see how to get this using the calculator.

What if you do not have an advanced calculator and you cannot get the fractional part in this way? It is simple. For example,  \(\frac{59}{3}=19.666667\). Just subtract \(19.666667-19\) , to remove the integer part, then multiply 0.666667 by 3. So, the remainder will be 2.

The same in \(\frac{19}{3}=6.333333\). So, if you do \(6.33333 – 6\) , then multiply 0.3333 by 3, the remainder will be 1.

Steps to convert the fractional part of the decimal number to ternary:

1. we will multiply the fractional part by 3 and write the integer part in the integer column.
2. continue the multiplication process. However, there is something new. In this example, you will never reach zero. You will continue in the multiplication process forever. So, when will you stop?

If you are a student, your professor must determine the precision as you will see in the next example.

Now, the question is, when will the computer stop? Of course, the computer cannot continue forever, because this needs a computer with a memory that increases forever. Of course, this is impossible.

But each computer is designed to store a certain number of bits, and it stops at this number of bits. If you do not understand this now, do not worry, we will talk about it in this course?

Now, we can write

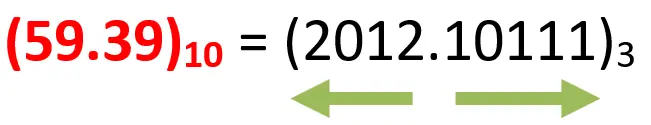
In the integer part: the remainder is always from 0 to 2.

In the fractional part: the integer part resulting from the multiplication is always from 0 to 2.

The general algorithm for converting from decimal number system to any number system (i.e., base-n number system):

Because we used the same method in all previous examples, we can extract a general algorithm for conversion from the decimal number system to any other number system.

A) Converting the integer part:

1. Divide the integer part by the base (n) of the number system we convert to.
2. Calculate the remainder in each division process by multiplying the resulting fractional part by the base (n) of the number system we convert to. Then write the remainder in the remainder column.
3. Continue in the division process until the resulting integer part becomes less than the base (n).
4. Write the remainder from top to bottom and from right to left, starting next to the decimal point.

B) Conversion of the fractional part:

1. Multiply the fractional part by the base (n) of the number system we convert to.
2. Write the resulting integer part in the integer column.
3. Continue the multiplication process of the fractional part and repeat step 2 each time.
4. Write the integer part from top to down and from left to right starting from the decimal point.

c) Conversion from the decimal number system to the Quaternary number system:

The quaternary number system (also called base-4 number system) has only 4 digits; 0 to 3.

The Successive division method:

Example 11:

What is the equivalent quaternary number of the decimal number (59.39)₁₀ system with precision up to 5 digits?

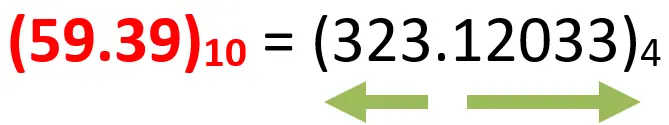
In the integer part: the remainder is always from 0 to 3.

In the fractional part: the integer part resulting from the multiplication is always from 0 to 3.

d) Conversion from the decimal number system to the Octal number system:

Here, we will not explain the example in detail as before, but you can watch the video.

The Successive division method:

Example 12:

What is the equivalent Octal number of the decimal number (59.39)₁₀ with precision up to 5 digits?

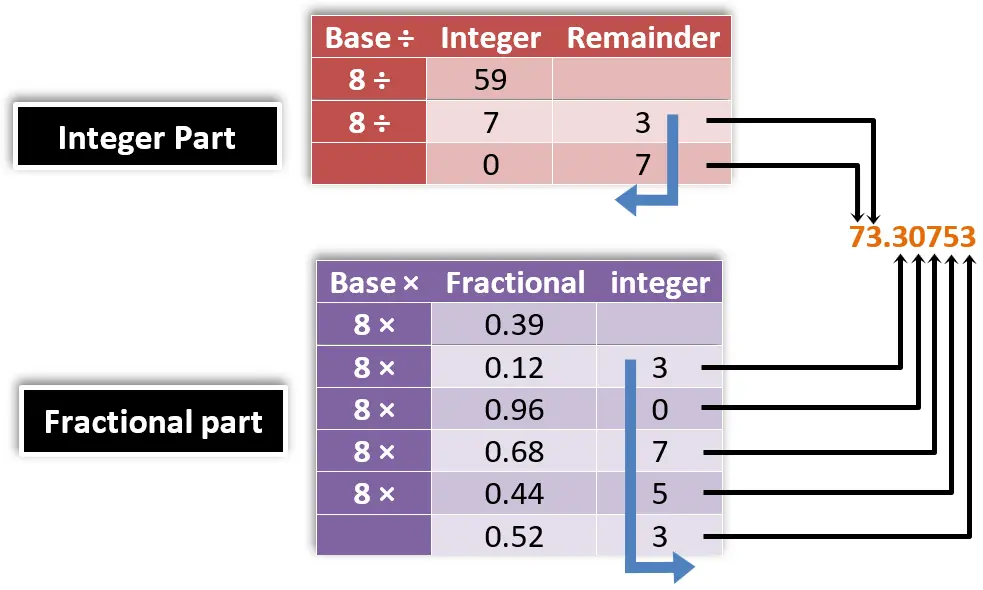
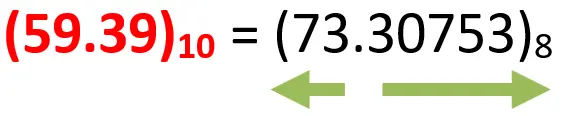
In the integer part: the remainder is always from 0 to 7.

In the fractional part: the integer part resulting from the multiplication is always from 0 to 7.

e) Conversion from the decimal number system to the Hexadecimal number system:

Here, we will not explain the example in detail as before, but you can watch the video on the channel.

The Successive division method:

Example 13:

What is the equivalent hexadecimal number of the decimal number (59.39)₁₀ with precision up to 5 digits?

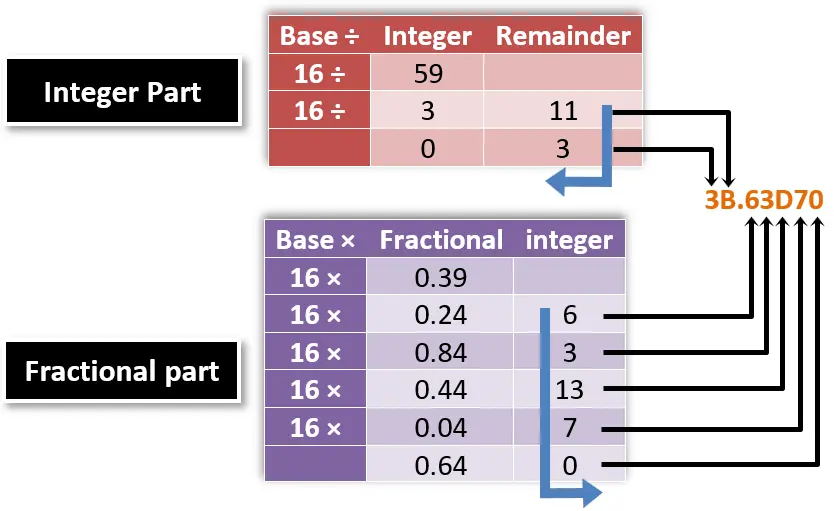
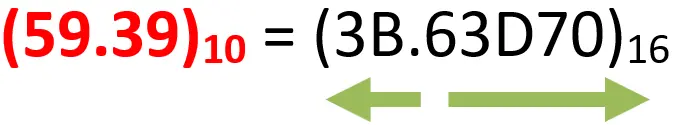
Notice that this time the remainder is 11 because we convert to the hexadecimal number system. So, 11 is not written as 11, but it is written as B. As we said in lesson 2, we cannot consider 11 as one digit; so, from 10 we give letters as follow:

A = 10, B = 11, C = 12, D = 13, E = 14, F = 15

The same in the fractional part, 13 is written as D.

In the integer part: the remainder is always from 0 to 15.

In the fractional part: the integer part resulting from the multiplication is always from 0 to 15.