1.2) تمثيل ارقام النظام العشري بالنظام الثنائي (binary language)
عرفنا اننا عشان نكلم الكومبيوتر بلغته لازم نبقى عارفين اذاي نترجم او نحول كل حاجة في لغتنا من ارقام وحروف وعلامات خاصة الى صفر وواحد واللى هي لغة الكومبيوتر. وهنبدا بتحويل الأرقام الى اصفار ووحايد وعشان نعمل ده لازم نعرف الأول اذاي الأنظمة العددية بتشتغل عن طريق معرفة اذاي النظام العشري بيشتغل…
1.2) الأنظمة العددية (Number Systems):-
لما بنقول هنتعلم تحويل الأرقام الى اصفار ووحايد، اكيد طبعا هيجي في بالك اننا هنحول الأرقام بالنظام العشري اللى بنستخدمه كل يوم الى اصفار ووحايد.
ده صحيح … ولكن لازم ناخد بالنا من نقطتين:
- الصفر والواحد ده سمناه binary language وقولنا عليه لغة الكومبيوتر ولكن هو برضو نظام عددي واسمه النظام الثنائي
- احنا مشبس هناخد التحويل من النظام العشري للنظام الثنائي فقط ولكن فيه أنظمة عددية تانية مستخدمة في علوم الحاسب.
الحقيقة فيه أنظمة عددية كتيرة جدا وتقدر تشوفها في اللينك ده (اضغط هنا)
لكن احنا يهمنا الأنظمة العددية الموضحة في الجدول التالي:
| الانظمة العددية | الاساس | الرموز |
|---|---|---|
| النظام العشري (Decimal) | 10 | 0,1,2,3,4,5,6,7,8,9 |
| النظام الثنائي (Binary) | 2 | 0,1 |
| النظام الثلاثي (Ternary) | 3 | 0,1,2 |
| النظام الثماني (Octal) | 8 | 0,1,2,3,4,5,6,7 |
| النظام السداسي عشر (Hexadecimal) | 16 | 0,1,2,3,4,5,6,7,8,9, A, B, C, D, E, F |
خلينا نفهم الجدول ده مع بعض…
الجدول احنا بنتكلم فيه عن 5 أنظمة عددية…
كلمة base معناها الأساس … بمعنى ايه … النظام العشري الأساس بتاعه 10 … ليه؟ … عشان بيتكون من 10 ارقام تحت العشرة; من 0 الى 9 ، وخلينا بدل مانقول رقم تحت العشرة نقول رمز او digit وهنعرف عليه… ونفس الكلام لما أقول ان الأساس للنظام الثنائي هو 2 معناها انه بيتكون من رمزين فقط او 2 digits؛ هما 0 و1 وكذلك لما أقول الأساس للنظام الثلاثي او الternary number system هو 3 معناها انه بيتكون من 3 digits فقط من 0 الى 2 …. وده الموضح في الجدول
وطبعا نفس الكلام للنظام الثماني (Octal number system)، الأساس بتاعه 8 يعنى بيتكون من 8 digits من 0 الى 7… وعندنا كمان النظام السداسي عشر (Hexadecimal number system) بيتكون من 16 رقم ويشمل الأرقام من 0 ل15.
ولكن فيه مشكلة النظام السداسي عشر، ان مينفعش أقول على ال15 رمز او digit يعنى … وخد بالك ان فيه فرق بين كلمة digit وبين كلمة number .. ال2 بمعنى رقم ولكن الdigit بيعبر عن رقم او رمز واحد فقط من 0 الى 9 لكن number بيعبر عن رقم ليه قيمة مهما كان اكبر من 9 … وعشان كدة قولنا خلينا نقول رمز و digit عشان نفرق
وبما ان الdigit بيعبر عن رقم واحد او رمز واحد فقط فإذن ال15 مكونة من 2 digits اللى هما ال1 وال5 وده مينفعش في الكومبيوتر بمعنى مينفعش اعبر عن رمز واحد برمزين مع بعض ولازم نلاقي طريقة نقدر نعبر بيها عن ال15 برمز واحد فقط مش2 بمعنى عايزين طريقة نعبر بيها عن ال15 كone digit…. فقالو الحل اننا من اول10 هندي حروف .. يعنى كدة
A = 10, B = 11, C = 12, D = 13, E = 14, F = 15
طيب هل هنقدر نحول من أي نظام للbinary او الdecimal او من أي نظام للتاني… اه ينفع وهو ده اللى احنا هنعمله في الشابتر ده…
ولكن عشان نقدر نعمل تحويل من نظام عددي للتاني، هنبقى محتاجين نعرف الطريقة العامة اللى بيشتغل بيها أي نظام عددي … وعشان نقدر نستنتجها مع بعض لازم نشوف الطريقة اللى بيشتغل بيها النظام العشري اللى بنستخدمه كل يوم … وهو ده اللى هنعمله
والقاعدة العامة اللى هنعملها هنسميها base-n number system…. بحيث n تعبر عن الأساس او الbase للنظام العددي.
1.2.1.1) النظام العشري (Decimal number system)
اول حاجة خلينا نتفق ان النظام العشري (decimal number system) سميناه بالاسم ده عشان هو بيتكون من 10 رموز من 0 الى 9 … وبنقول عليه بالعربي نظام عددي أساسه هو 10 او بالانجليزي بنقول عليها base-10 number system.
أ) كيفية العمل بالنظام العشري:
خلينا ناخد رقم صحيح كمثال وليكن 159 … الرقم ده مكون من 3 رموز بنقول عليهم بالانجليزي 3 digits … وخلاص عرفنا الفرق بين الdigit والnumber.
ولكن اذاي ال3 رموز دول لما اتحطو جنب بعض ادونا القيمة مائة وتسعة وخمسون …
كل digit او رمز من ال3 بياخد قيمة (بنسميها weight او وزن يعنى) طبقا لمكانه او موقعه …. خلينا نشوف الجدول التالي عشان نفهم اكتر:
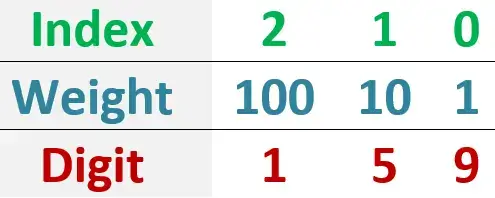
الindex هي ترقيم او موقع الdigit داخل ال159 او يعنى داخل الnumber. وخد بالك اننا بنرقم من اليمين للشمال وبنبدا الترقيم من الصفر
فاكر لما كنا بنقول اول خانة هي خانة الاحاد والتانية خانة العشرات والتالتة خانة المئات وهكذا … الحقيقة اننا بنقول كدة عشان ال159 ناتجة من ضرب كل رمز في قيمته او وزنه اللى بياخدها من موقعه داخل الnumber وبعد كدة بنجمع نواتج الضرب دي في الاخر … يعنى كدة
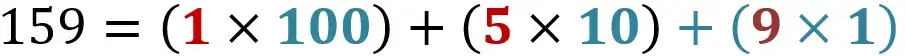
تلاحظ ان وزن كل digit طبقا لموقعه بتكون ناتج ضرب 10 في وزن الموقع اللى قبله … يعنى مثلا ال5 وزنها ب10 لانها في خانة العشرات ووزن ال ال1 المضروب في 100 جاية من ضرب 10 في وزن ال5 اللى هي 10 يعنى 10×10 ب100
طيب ايه رايك لو عملناها كدة

القيمة متغيرتش …. طيب تلاحظ ايه … الاس اللى فوق ال10 عند كل رمز هو موقع الرمز نفسه او الindex بتاعه …. طيب تعالي نكتبهم فوق كل رقم
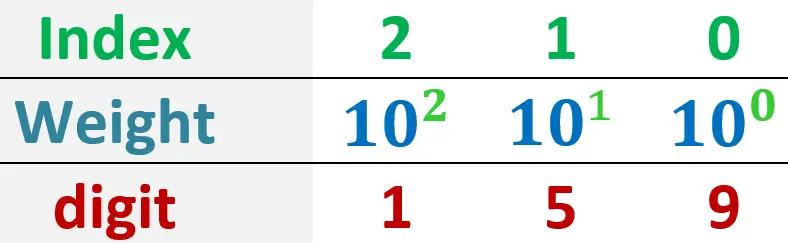
ذي مانت شايف، االوزن اللى فوق كل رقم عبارة عن 10 مرفوعة لاس الindex او موقع الdigit في الرقم.
طيب معلش ولو كان فيه كسر … بنعمل ايه… تعالى نزود كسر للرقم اللى عندنا ده وليكن 159.25 … كل اللى بيختلف بس ان الترقيم بيبدا من -1 ومن الشمال لليمين ووزن كل رمز في الكسر بتبقى ناتجة عن قسمة وزن الرمز اللى قبله على 10 يعنى مشبنضرب في 10 … يعنى كدة
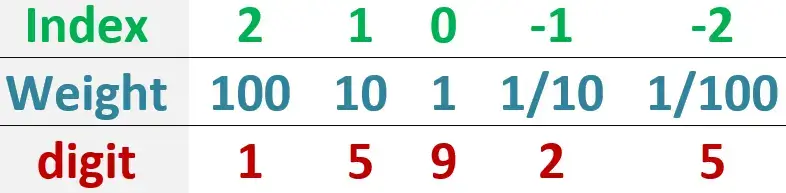
طيب خلينا نضربهم في 10 مرفوعة لاس الindex يعنى كدة

وطبعا أي حاجة مرفوعة لاس بالسالب معناها بنقسم يعنى 10-1 = 1/10
اخدت بالك …. طيب ايه رايك … ممكن تستنج ايه من الكلام ده؟
- انت بتضرب كل رمز في 10 مرفوعة لاس الترقيم بتاعه
- الترقيم بتاع الجزء الصحيح بيبدا من عند العلامة العشرية وبيبدا من 0 وبنستمر من اليمين للشمال والترقيم في الكسر بيكون من عند العلامة العشرية من الشمال لليمين وبيبدا من -1
- كل ما بنضيف رمز زيادة في الجزء الصحيح بنضرب في 10 وكل ما بنضيف رمز زيادة في الكسر بنقسم على 10.
طيب اشمعنى 10 … عشان دي الأساس بتاع النظام العشري يعنى عشان بيتكون من 10 ارقام (10 digits) ….
ب) خوارزمية عامة لاي نظام عددي (طريقة عمل اي نظام عددي):
طيب خلينا نعمم الكلام ده على أي نظام عددي (number system).
- كل رمز بينضرب في وزن طبقا لموقعه والوزن ده بيساوي الأساس بتاع النظام العددي وليكن رمزه (n) مرفوع لاس الترقيم بتاع الرقم (index) وليكن رمزه (i) يعنى كدة

- بعد كدة حاصل جمع عمليات الضرب دي بتكون هي القيمة او الnumber المقصود …
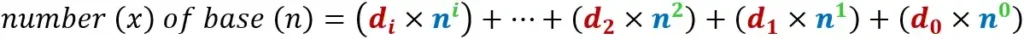
فلو رمزنا للترقيم ب(i) اختصارا لindex … هيبقى المعادلة العامة كالتالي:
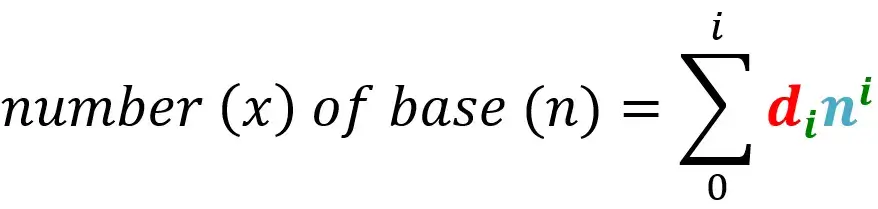
1.2.1.2) النظام الثنائي (binary number system)
أ) استخدام الخوارزمية العامة (الطريقة العامة) للتحويل من النظام الثنائي الى النظام العشري:
طيب خلينا نطبق القاعدة العامة دي على النظام الbinary اللى بيتكون من صفر وواحد فقط …. وبما انه بيتكون من رمزين فقط يبقى الأساس بتاعه 2 يعنى الn = 2 يعنى نقدر نكتب كدة
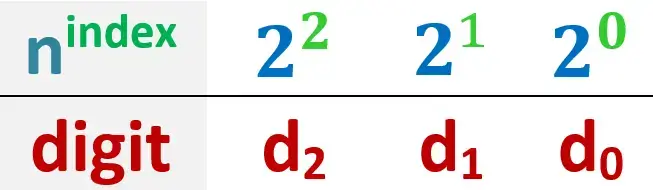
طيب ايه رايك لو كتبنا قيمة كل أساس بعد ما نرفعه للاس بتاعه
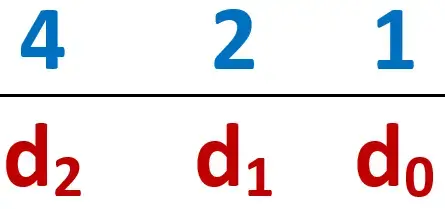
طيب الd هنا اقدر اشيلها واحط ايه؟ … في النظام الbinary هتحط فقط ال0 وال1 … وبنسمي ال0 وال1 bits ودي اختصار الى binary digits.
خلينا ناخد مثال
مثال 1:
ما هي قيمة الرقم الثنائي التالي: 2(100) في النظام العشري؟
الحل
| 22 | 21 | 20 |
| 4 | 2 | 1 |
| 1 | 0 | 0 |
(100)_2=(1×2^2 )+(0×2^1 )+(0×2^0 )=4+0+0=(4)_{10}تلاحظ اننا بنكتب 2 بخط صغير من تحت ذي كدة 2(100) عشان نميز ان ال100 ده رقم يتبع النظام الثنائي (binary number system) وليس النظام العشري (decimal number system) وكتبنا 10 بخط صغير تحت ال4 يعنى كدة 10(4) عشان نوضح ان ال4 هنا هي عدد في النظام العشري …
مثال 2:
ما هي قيمة الرقم الثنائي التالي: 2(110) في النظام العشري؟
الحل
| 22 | 21 | 20 |
| 4 | 2 | 1 |
| 1 | 1 | 0 |
(110)_2=(1×2^2 )+(1×2^1 )+(0×2^0 )=4+2+0=(6)_{10}خوارزمية التحويل من النظام الثنائي الى لنظام العشري (Algorithm of conversion from binary number system to decimal number system)
من الأمثلة دي نقدر نستنتج خطوات التحويل من binary الى decimal عادي … اذاي؟
- هتكتب فوق كل رمز من اليمين للشمال الأساس مرفوق لاس الترقيم او ممكن تكتب 1 علطول عند اول رمز من اليمين وهتضرب في 2 وانت ماشي من اليمين للشمال.
- تجمع الأرقام اللى تحتها 1 فقط
خلينا ناخد مثال كمان عشان نفهم الطريقة دي:
مثال 3:
ما هي قيمة الرقم الثنائي التالي: 2(1110) في النظام العشري؟
الحل
| 23 | 22 | 21 | 20 |
| 8 | 4 | 2 | 1 |
| 1 | 1 | 1 | 0 |
اول خطوة عملناها اننا كتبنا فوق الرموز 1 2 4 8 وتلاحظ اننا بنضرب في 2، وطبعا اشمعنى 2 عشان ده الأساس بتاع الرقم الbinary يعنى عشان بيتكون من رمزين فقط … ولو زودنا رمز تاني من ناحية الشمال هنضرب ال8 في 2 فهتبقى 16 وهكذا.
تاني خطوة هي انك تجمع الأرقام اللى فوق الوحايد فقط … يعنى كدة
(1110)_2=8+4+2 =(14)_{10}تعالى نخلي الموضوع اسهل ونعملها في جدول
| × | 8 | 4 | 2 | 1 | |
| 1 | 1 | 1 | 0 | Sum (14)10 | |
| = | 8 | 4 | 2 | 0 |
من الأمثلة دي نقدر نقول الاتي … ان ال 2(100) هو تمثيل النظام الثنائي او الbit pattern للرقم 4 في النظام العشري وان ال 2(110) هو الbit pattern للرقم 6 في النظام العشري وال 2(1110) هو الbit pattern للرقم 14 في النظام العشري.
وطيب بالنسبة لو فيه كسر في الرقم الbinary … تعالى ناخد مثال.
مثال 4:
ما هي قيمة الرقم الثنائي التالي: 2(1110.01) في النظام العشري؟
الحل
| 23 | 22 | 21 | 20 | 2-1 | 2-2 | |
| 8 | 4 | 2 | 1 | ¼ | ||
| 1 | 1 | 1 | 0 | . | 0 | 1 |
خلاص فهمنا الطريقة … بس هنا في الكسر هنقسم على 2 طبعا لان n = 2 عشان ده النظام الثنائي.
(1110.01)_2=8+4+2+(1/4) =(14.25)_{10}طيب خلينا نعملها بالجدول اسهل
| × | 8 | 4 | 2 | 1 | ½ | ¼ | ||
| 1 | 1 | 1 | 0 | . | 0 | 1 | Sum (14.25)10 | |
| = | 8 | 4 | 2 | 0 | 0 | ¼ |
بس خد بالك … العلامة العشرية في النظام الbinary مشبتتخزن في الكومبيوتر كنقطة كدة … احنا لحد الان بناخد طريقة تمثيل البيانات بالاصفار والوحايد على الورق لكن لسة متكلمناش عن طريقة التخزين الفعلية في الكومبيوتر بتم اذاي.
