1.2.2.2) التحويل من النظام العشري الى أي نظام عددي اخر
أ) التحويل من النظام العشري الى النظام الثنائي: (decimal to binary conversion)
فيه عندي 3 طرق للتحويل من النظام العشري الى النظام الثنائي …
طريقة القسمة المتتالية (Successive divisions)
دي الطريقة الرسمية او الformal اللى هتلاقيها في المراجع وهتاخدها في الجامعة وهتحل بيها في الامتحانات. تعالى ناخد مثال ونكتب بعد كدة خوارزمية الحل او طريقة الحل.
مثال 9:
?What is the equivalent binary number of the decimal number (21.25)10
احنا بنحول الجزء الصحيح لوحده والكسر لوحده كالتالي:
بالنسبة للجزء الصحيح (integer):
لما كنا بنحول من binary لdecimal كنا بنضرب كل رقم binary في 2 مرفوعة لاس ترقيمه في الرقم … لما نيجي نحول للعكس هنقسم على 2 مشهنضرب … طيب هنعمل ايه هنا.
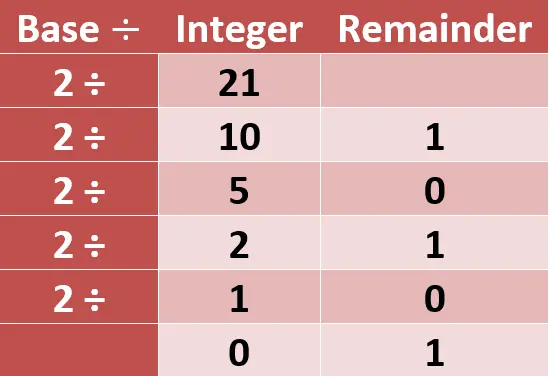
خطوات الحل:
- هقسم ال21 على الbase بتاع الbinary لان ده هو النظام اللى هحول ليه …. فهتبقى ب10.5 وطالما فيه كسر يبقى القسمة ليها باقي قسمة … اللى هو بنسميه بالانجليزي الremainder …
- طيب وبعدين … هعمل ايه بباقي القسمة بعد كدة … هنحطه في عمود لوحده في الجدول هنسميه الremainder … وهنكمل قسمة الرقم الصحيح على 2.
- وبعد كدة همسك ال10 او الجزء الinteger واحطه في خانه الinteger وهقسمه على 2 هيبقى الناتج 5 … طيب هل هنا فيه باقي قسمة؟؟؟ ….. لا طبعا … يبقى في خانة الremainder هحط 0 …
- همسك ال5 هقسم على 2 … هتبقى ب2.5 ..يبقى هكتب ال2 في عمود الinteger وباقي القسمة بيساوي 1 وهكتبه في عمود الremainder …
- طيب 2 على 2 ب1 ومفيش خارج قسمة يبقى هحط 0 في الremainder و1 في عمود الinteger…
- هقسم 1 على 2 … هتبقى ب 0.5 … طيب هنا في جزء integer … لا طبعا … يبقى هحط في الinteger 0 … طيب والremainder هحط 1 … لانه أصلا لسة ال1 يعتبر ملوش قسمة صحيحة على 2 …. وكقاعدة …. أي كسر باقي قسمته هو البسط …. وطالما وصلت للصفر في الجزء الinteger يبقى انا كدة خلصت الجزء الinteger.
نكتب خوارزمية تحويل الجزء الصحيح (integer part) من النظام العشري الى النظام الثنائي:
- الخطوة الأولى – اقسم الجزء الصحيح على 2
- الخطوة الثانية – اكتب باقي القسمة – اللى هنسميها remainder – في العمود الخاص بالremainder والجزء الصحيح في العمود الخاص بالجزء الInteger. إذا لم يكن هناك باقي من القسمة، اكتب 0 في عمود الremainder.
- الخطوة الثالثة – كرر الخطوات السابقة في قسمة الجزء الصحيح الناتج من القسمة الى ان يصبح الجزء الصحيح 0.
كيفية حساب باقي القسمة بسهولة:
طيب انا اعرف باقي القسمة اذاي؟؟
همسك الكسر الناتج من عملية القسمة واضربه في أساس النظام اللى بحول ليه … بمعنى لما كان الناتج 10.5 فهضرب ال0.5 في 2 (عشان أساس النظام الثنائي) وهيكون الناتج 1 وهو ده باقي القسمة.
لو وصلت ان في القسمة البسط اقل من المقام يبقى باقي القسمة هو البسط والجزء الصحيح هيبقى ب0.
وخد بالك بما انك بتحول الى لنظام الثنائي فدايما هتلاقي باقي القسمة اما 1 او 0 فقط.
بالنسبة للكسر:
في التحويل من النظام الثنائي الى النظام العشري، لما كنا بنحول الكسر كنا بنقسم على 2 فهنا بقى التحويل للعكس من النظام العشري الى النظام الثنائي يبقى هنضرب مشهنقسم.
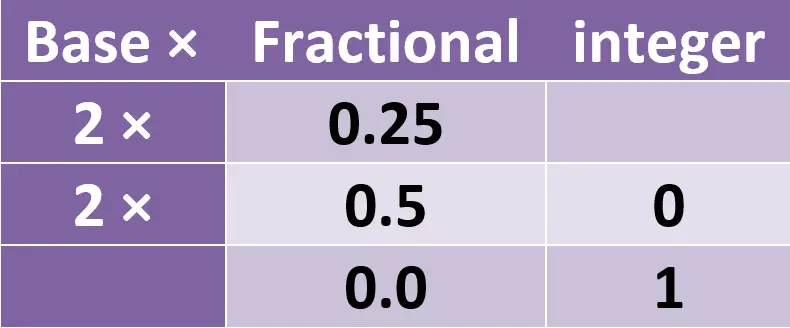
هضرب في الbase اللى هي ال2 …
خطوات الحل:
- هضرب 0.25 في 2 هتبقى 0.5 …
- هل هنا فيه جزء integer او رقم صحيح بعد الضرب … مفيش … يبقى هحط 0 في خانة الinteger في الجدول ….
- وبعد كدة هضرب 0.5 في 2 هتبقى ب1.00 هاخد ال1 عشان integer وهحطه في خانة الinteger
- بما ان الكسر بيساوي 0 او مفيش كسر يعنى يبقى المسألة خلصت.
ولاحظ ان الجزء الصحيح اللى هيطلع من الضرب دايما هيكون اما 0 او 1.
نكتب خوارزمية تحويل الكسر (fractional part) من النظام عشري الى النظام ثنائي:
- الخطوة الأولى – اضرب الكسر في 2
- الخطوة الثانية – اكتب الجزء الصحيح الناتج من عملية الضرب في عمود الinteger والكسر في عمود الfraction …. لو كان ناتج الضرب لا يحتوى على جزء صحيح، إذن اكتب 0 في عمود الInteger.
- الخطوة الثالثة – كرر الخطوات السابقة في ضرب الكسر الى ان تصل الى 0 او تصل الى الدقة المطلوبة (عدد الdigits المطلوب بعد العلامة العشرية).
كيفية كتابة النتيجة النهائية من الجداول:
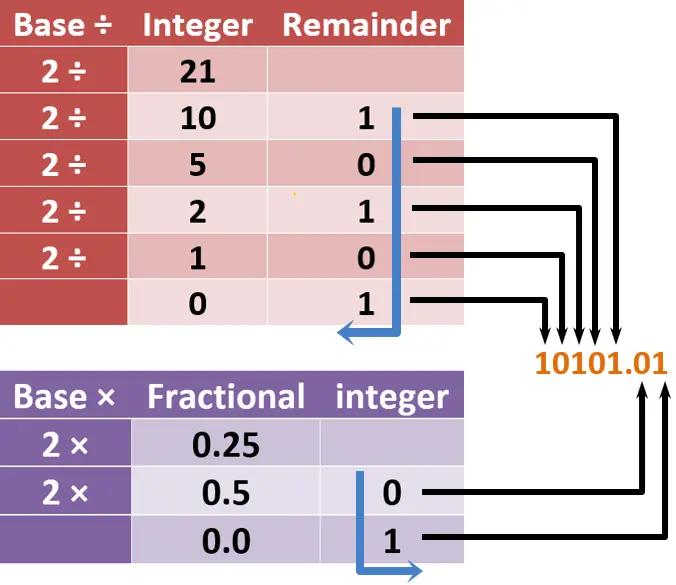
الأول طبعا هنكتب علامة عشرية
______.___
وبعد كدة همسك الجزء الinteger … هكتب الأرقام من فوق لتحت ذي ما هو موضح بالسهم الازرق من جنب العلامة العشرية وبمشى جهة الشمال.
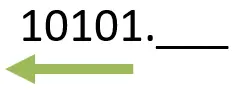
وبعد كدة همسك الجزء الfraction وهكتب الأرقام من فوق لتحت ولكن هبدأ من جنب العلامة العشرية مباشرة وبمشى جهة اليمين.
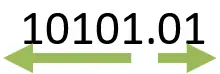
وبالتالي نقدر نكتب الاتي
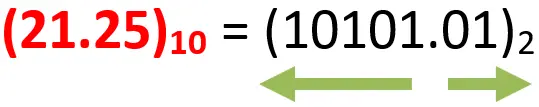
طيب بالنسبة للتحويل من الdecimal إلى أي نظام …. هنعمل نفس الكلام مع اختلاف اننا هنضرب او هنقسم على حسب الbase بتاعة النظام اللى هنحول ليه … وبالتالي مشهنشرح كل الخطوات دي وكل الكلام ده في كل مثال.
ب) التحويل من النظام العشري الى النظام الثلاثي: (decimal to ternary conversion)
ناخد بالنا من نقطة … ان التحويل من النظام العشري (decimal number system) الى أي نظام عددي اخر بتكون بنفس الطرق السابقة بالظبط مع اختلاف تغيير الbase … يعنى بدل ما كنا بنقسم او بنضرب في 2 هنقسم او هنضرب في الbase بتاع النظام العددي اللى بنحول ليه.
طريقة القسمة المتتالية (Successive divisions)
مثال 10:
?What is the equivalent ternary number of the decimal number (59.39)10
احنا بنحول الجزء الصحيح لوحده والكسر لوحده كالتالي:
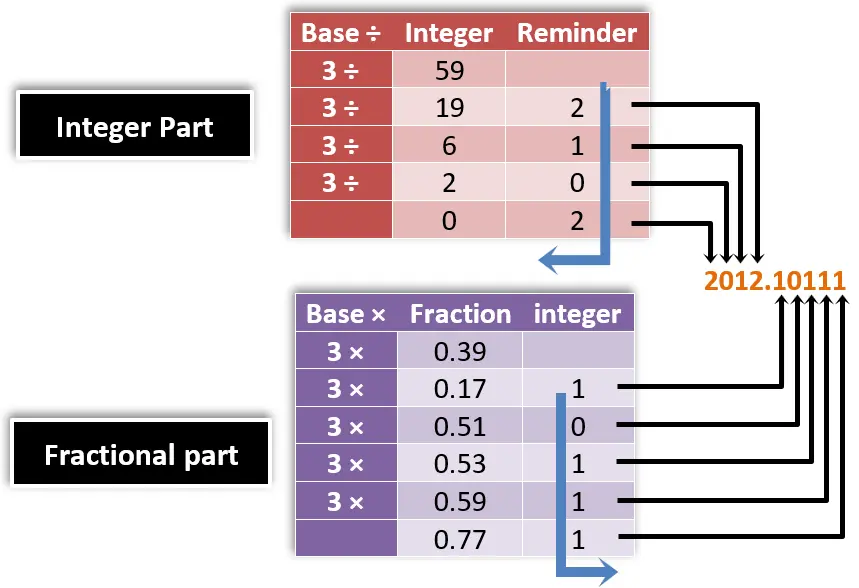
خطوات تحويل الجزء الصحيح (integer part) من النظام العشري الى النظام الثلاثي:
- بنقسم الجزء الصحيح على 3 وباقي القسمة بنكتبه في عمود الremainder اللى هو باقي القسمة
- هنكمل قسمة لحد ما نوصل ل … في الحالة دي هيكون الجزء الصحيح 0 وبالتالي نكون وصلنا لنهاية عملية القسمة وهيكون باقي القسمة هو 2.
كيفية حساب باقي القسمة بسهولة:
طيب بجيب باقي القسمة اذاي …. انا هنا لما قسمت كان الناتج … عشان تجيب الكسر بالطريقة المكتوبة دي … شوف الفيديو على القناة هنعرفك اذاي تجيبها بالالة الحاسبة … ولكن مش شرط تكتب الكسر كدة يعنى لو بالة حاسبة عادية هيبقى ناتج القسمة 19.6666 … اطرح 19 هيتبقى عندك 0.6666 اضربها في 3 هيبقى باقي القسمة 2 … ولو ضربت في 3 هيبقى باقي القسمة 2 برضو.
ونفس الكلام لما تقسم هيكون الناتج … يعنى 6.3333 … فلو طرحت 6 … هيتبقى 0.33333 لما تضربها في 3 هيبقى باقي القسمة هي 1 … وكمل بنفس الطريقة لحد ما توصل ل2/3 … الجزء الinteger هيكون 0 لان 2/3 بتساوي 0.66666 ويكون باقي القسمة هو البسط ذي ما قولنا قبل كدة …. يعنى باقي القسمة هو 2.
خطوات تحويل الكسر (Fractional part) من النظام العشري الى النظام الثلاثي:
- هنضرب الكسر في 3 اللى هو أساس النظام الثلاثي ونكتب الجزء الصحيح في عمود الInteger والfraction في عمود الfraction.
- تستمر في عملية الضرب ولكن المثال هنا فيه حاجة جديدة … عملية الضرب هتستمر للابد ومشهتوصل للصفر … وهنا نسال نفسنا سؤال مهم…. هنقف لحد فين؟
لو انت طالب في الكلية فلازم الدكتور بتاعك يقولك هتقف لحد مثلا 5 ارقام بعد العلامة العشرية وبيقولها بالانجليزي في السؤال كدة (with precision up to 5 digits)…
طيب في الحقيقة … الكومبيوتر بيقف لحد فين … اكيد مشبيفضل يزود ارقام بعد العلامة العشرية الى ما لا نهاية لانه عشان يعمل ده يبقى لازم الذاكرة بتاعته برضو هي كمان تكون بتكبر الى مالانهاية وده مشموجود ومستحيل عمليا.
لكن الكومبيوتر وقت تصميمه بيكون متحدد هو اخره بيعرض كام bit يعنى بنحددله عدد الBits اللى بيقدر يخزنها ويعرض بيها الداتا … وده هنتكلم عنه قدام في الكورس برضو.
يبقى اذن
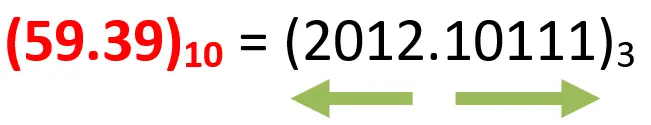
في تحويل الجزء الصحيح: دايما هتلاقي باقي القسمة من 0 الى2
في تحويل الكسر: دايما الجزء الصحيح اللى هيطلع من الضرب دايما هيكون من 0 الى2
ت) التحويل من النظام العشري الى النظام الرباعي: (decimal to Quaternary conversion)
هناخد مثال واحد فقط بالطريقة الرسمية وهنشرح امثلة كتير بال3 طرق على القناة.
احنا مشهنشرح بالتفصيل خلاص لان الطريقة واضحة … لكن ممكن تشوف الفيديو على القناة.
النظام الرباعي (quaternary) بيتكون من 4 ارقام (4 digits) من 0 الى 3.
طريقة القسمة المتتالية (Successive divisions)
مثال 11:
?What is the equivalent quaternary number of the decimal number (59.39)10 system with precision up to 5 digits

في تحويل الجزء الصحيح: دايما هتلاقي باقي القسمة من 0 الى3
في تحويل الكسر: دايما الجزء الصحيح اللى هيطلع من الضرب دايما هيكون من 0 الى3
ث) التحويل من النظام العشري الى النظام الثماني: (decimal to Octal conversion)
هناخد مثال واحد فقط بالطريقة الرسمية وهنشرح امثلة كتير بال3 طرق على القناة.
احنا مشهنشرح بالتفصيل خلاص لان الطريقة واضحة … لكن ممكن تشوف الفيديو على القناة.
طريقة القسمة المتتالية (Successive divisions)
مثال 12:
?What is the equivalent Octal number of the decimal number (59.39)10 with precision up to 5 digits
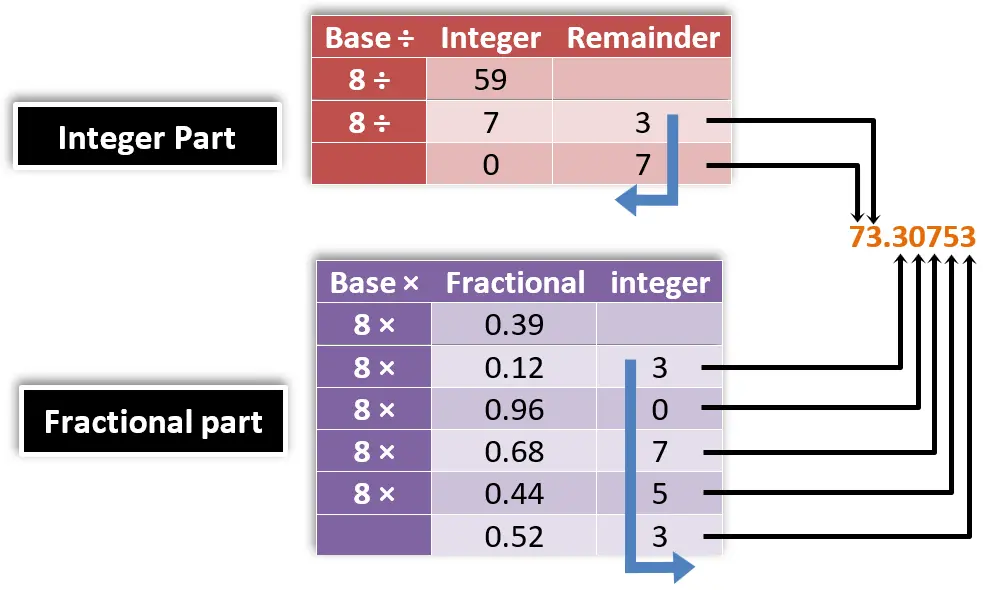
في تحويل الجزء الصحيح: دايما هتلاقي باقي القسمة من 0 الى7
في تحويل الكسر: دايما الجزء الصحيح اللى هيطلع من الضرب دايما هيكون من 0 الى7
ج) التحويل من النظام العشري الى النظام السداسي عشر: (decimal to Hexadecimal conversion)
هناخد مثال واحد فقط بالطريقة الرسمية وهنشرح امثلة كتير بال3 طرق على القناة.
احنا مشهنشرح بالتفصيل خلاص لان الطريقة واضحة … لكن ممكن تشوف الفيديو .
طريقة القسمة المتتالية (Successive divisions)
?What is the equivalent hexadecimal number of the decimal number (59.39)10 with precision up to 5 digits
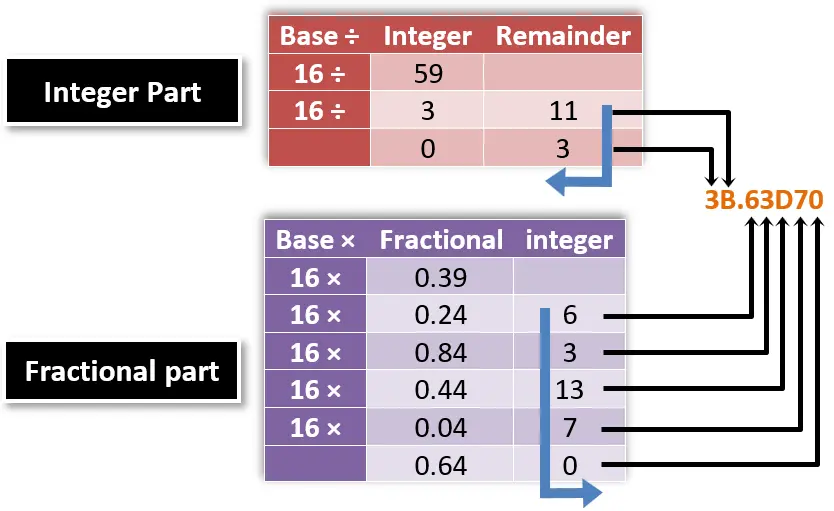
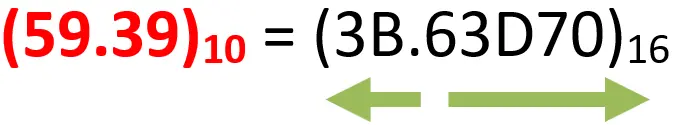
بس هنا خد بالك … في تحويل الجزء الصحيح، لقيت عندك 11 باقي قسمة … دي مشهتتكتب 11. افتكر اننا قولنا في النظام السداسي عشر فيه 16 رقم ومن اول ال10 بندي حروف
A = 10, B = 11, C = 12, D = 13, E = 14, F = 15
يبقى ال11 هتتكتب B وال13 اللى ظهرت في تحويل الكسر هتتكتب D.
في تحويل الجزء الصحيح: دايما هتلاقي باقي القسمة من 0 الى15
في تحويل الكسر: دايما الجزء الصحيح اللى هيطلع من الضرب دايما هيكون من 0 الى15
خوارزمية التحويل من النظام العشري الى أي نظام عددي اخر:
بما ان التحويلات اللى شوفناها في الأمثلة السابقة كلها شبه بعضها يبقى نقدر نطلع الطريقة العامة او الخطوات العامة او الالجوريزم العام اللى يخلينا نحول من النظام العشري الى أي نظام عددي اخر … خلينا نشوف الخطوات:
- أ) تحويل الجزء الصحيح (integer part):
- يتم قسمة الجزء الصحيح على أساس النظام العددي (n) اللى بنحول ليه.
- يتم حساب باقي القسمة (reminder) في كل مرة عن طريق ضرب الكسر في أساس النظام العددي (n).
- يتم استمرار قسمة الجزء الصحيح على أساس النظام العددي (n) الى ان يكون الجزء الصحيح اقل من (n)
- يتم كتابة باقي القسمة من اعلى الى اسفل وبدءا من العلامة العشرية الى جهة الشمال
- ب) تحويل الكسر (Fraction part):
- يتم ضرب الكسر في أساس النظام العددي (n)
- يتم كتابة الجزء الصحيح الناتج من عملية الضرب.
- يتم استمرار ضرب الكسر الناتج من عملية الضرب في كل مرة في أساس النظام العددي (n) ويتم كرار الخطوة رقم 2 كل مرة …
- يتم كتابة الأرقام الصحيحة الناتجة من عمليات الضرب من اعلى الى اسفل وبدءا من العلامة العشرية الى جهة اليمين.
